| Individuo | altezza [cm] |
| 1 | 175 |
| 2 | 174 |
| 3 | 158 |
| 4 | 183 |
| 5 | 191 |
| 6 | 177 |
| 7 | 173 |
| 8 | 179 |
| 9 | 179 |
| 10 | 168 |
| 11 | 166 |
| 12 | 170 |
| 13 | 173 |
| 14 | 170 |
| 15 | 169 |
| 16 | 190 |
| 17 | 180 |
| 18 | 171 |
| 19 | 167 |
| 20 | 166 |
| altezza [cm] |
| 158 |
| 166 |
| 166 |
| 167 |
| 168 |
| 169 |
| 170 |
| 170 |
| 171 |
| 173 |
| 173 |
| 174 |
| 175 |
| 177 |
| 179 |
| 179 |
| 180 |
| 183 |
| 190 |
| 191 |
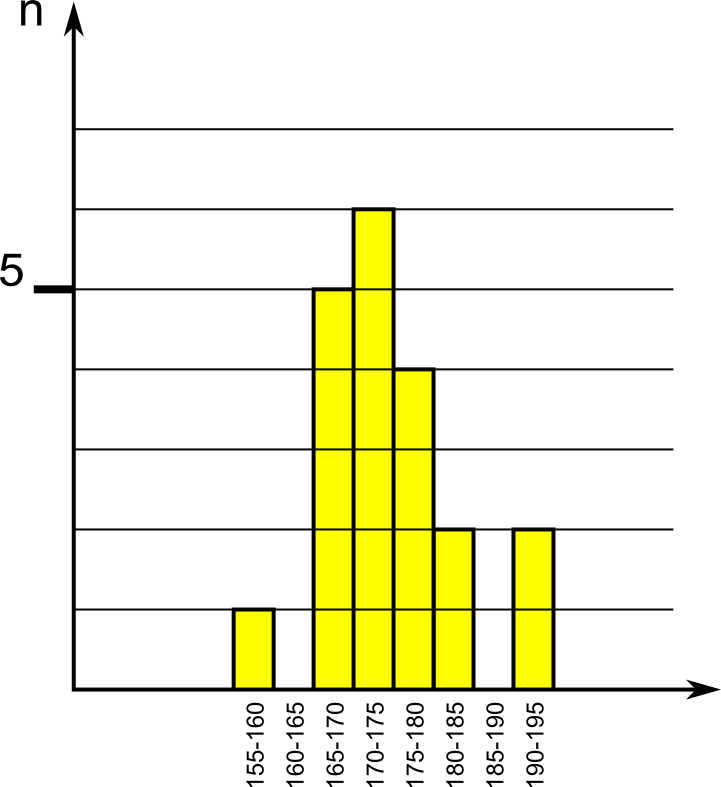
| classi di altezza [cm] valore inferiore compreso, valore superiore escluso |
numero di individui |
| 155-160 |
1 |
| 160-165 |
0 |
| 165-170 |
5 |
| 170-175 |
6 |
| 175-180 |
4 |
| 180-185 |
2 |
| 185-190 |
0 |
| 190-195 |
2 |
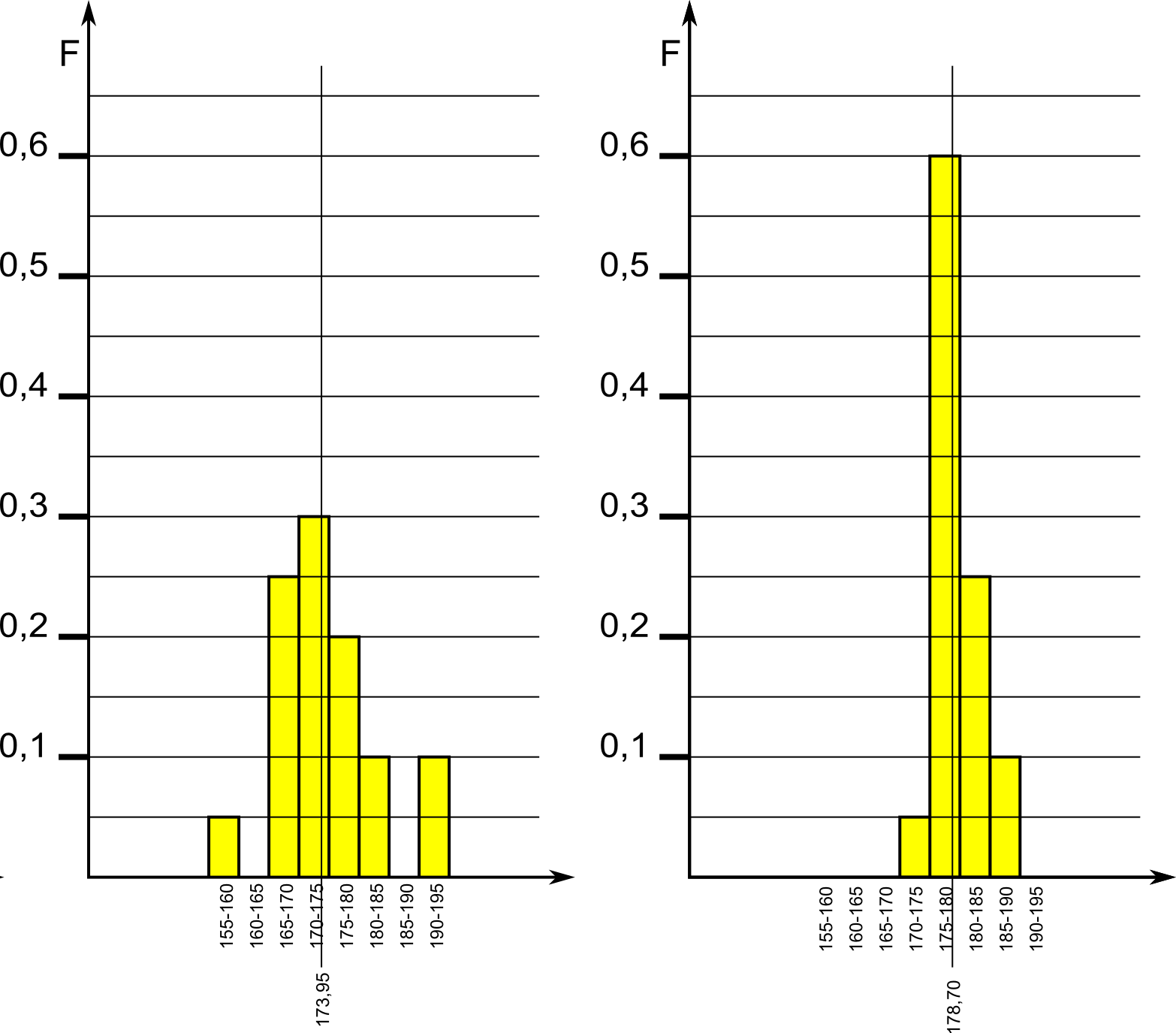
L'istogramma, così rappresentato, differisce solo per i valori indicati sull'asse verticale:

Rappresenta il valore della variabile più comune in una popolazione (in altre parole rappresenta la "classe" più popolata).
Nell'esempio fatto la moda è rappresentata dalla classe 170-175
Nell'esempio fatto la media dell'altezza della popolazione vale:
h = 173,95.
Spesso (ma non sempre) la media cade nella classe corrispondente alla moda.
Il significato pratico della media aritmetica è ben noto agli studenti, sempre impegnati a fare la media aritmetica dei propri voti! Rappresenta un valore molto significativo, appunto, medio, del valore della variabile all'interno di una certa popolazione.Attenzione che esistono altri tipi di media, oltre alla media aritmetica, ma non esiste una media chiamata "media matematica" (esiste la media geometrica, la media quadratica...).
Poiché la media aritmetica è la media più comune e semplice, di solito quando si parla di "media" senza specificare di che media si sta parlando, ci si riferisce implicitamente alla media aritmetica.
Si riferisce ad un singolo individuo, ed è semplicemente la differenza tra il valore della variabile per un certo individuo rispetto alla media
σi = xi - x
(σ è la lettera greca "sigma")
Attenzione al segno! Se la deviazione è positiva significa che il valore della variabile è maggiore della media, altrimenti è inferiore.L'individuo 1 è più alto della media (σ positiva), l'individuo 3 è invece più basso (σ negativo).
Si osservi che se si calcola la media aritmetica degli scarti, questa è ovviamente sempre zero. Questo perché, per definizione di media, i valori della variabile sono uniformemente distribuiti attorno alla media aritmetica.
σ = √[∑σi2/n] = √[∑(xi - x)2/n]
Per organizzare meglio i dati si può ad esempio completare la tabella del precedente esempio come segue, risulterà più facile calcolare lo scarto quadratico medio.
individuo |
altezza |
deviazione (rispetto alla
media di ciascun individuo): σi |
deviazione elevata al quadrato: σi2 |
| 1 | 175 | 1,05 | 1,1025 |
| 2 | 174 | 0,05 | 0,0025 |
| 3 | 158 | -15,95 | 254,4025 |
| 4 | 183 | 9,05 | 81,9025 |
| 5 | 191 | 17,05 | 290,7025 |
| 6 | 177 | 3,05 | 9,3025 |
| 7 | 173 | -0,95 | 0,9025 |
| 8 | 179 | 5,05 | 25,5025 |
| 9 | 179 | 5,05 | 25,5025 |
| 10 | 168 | -5,95 | 35,4025 |
| 11 | 166 | -7,95 | 63,2025 |
| 12 | 170 | -3,95 | 15,6025 |
| 13 | 173 | -0,95 | 0,9025 |
| 14 | 170 | -3,95 | 15,6025 |
| 15 | 169 | -4,95 | 24,5025 |
| 16 | 190 | 16,05 | 257,6025 |
| 17 | 180 | 6,05 | 36,6025 |
| 18 | 171 | -2,95 | 8,7025 |
| 19 | 167 | -6,95 | 48,3025 |
| 20 | 166 | -7,95 | 63,2025 |
| medie dei valori sovrastanti: |
173,95 | 0 | 62,9475 |
| radice quadrata della media (casella di sopra): | 7,93 |
La deviazione standard, o scarto quadratico medio,
è dunque
σ = √62,9475 = 7,93
Avvertenza importante! Attenzione agli arrotondamenti impropri! Nell'elevare al quadrato i valori σi sarà necessario tenere conto di una quantità doppia di cifre decimali rispetto a quelle degli stessi valori σi. Effettuando poi, come ultimo passaggio, la radice quadrata della media, sarà possibile, arrotondando correttamente, tornare ad avere il valore espresso con il numero di decimali iniziale.
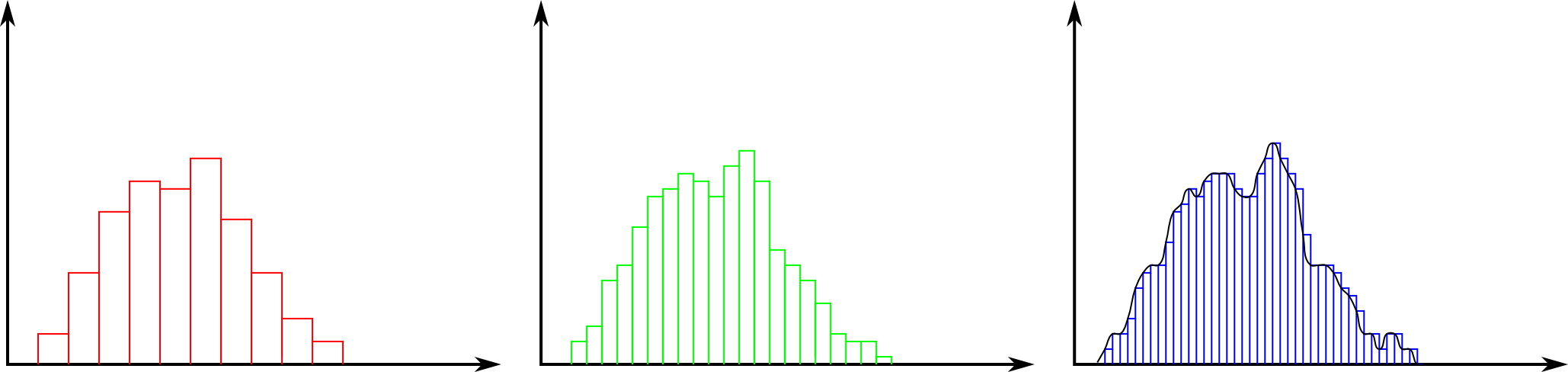
Quando una popolazione è molto grande si può pensare di suddividerla in moltissime classi sempre più piccole, e l'istogramma tende a diventare una curva che ha sull'asse orizzontale la variabile in esame "continua" (non più suddivisa in classi).

La rappresentazione di una variabile statistica di una popolazione attraverso un primo istogramma (in rosso). La stessa popolazione rappresentata in un istogramma (in verde) con classi di ampiezza 1/2 rispetto alla prima. La stessa popolazione rappresentata in un istogramma (in blu) con classi di ampiezza 1/4 rispetto alla prima. Al ridursi dell'ampiezza delle classi, l'istogramma tende sempre più a diventare una curva (in nero) che è la distribuzione limite.
In questo caso però non ha più molto senso indicare la frequenza sull'asse verticale, in quanto se prendiamo in esame classi sempre più piccole, anche la frequenza di ciascuna classe diventerà sempre più piccola, fino a tendere a zero.
Si utilizza perciò, al posto della frequenza F, la densità di frequenza f(x) che è il rapporto tra la frequenza (che se l'ampiezza della classe è molto piccola, è anch'essa molto piccola) e l'ampiezza della classe (che è assai piccola). Il rapporto tra due numeri entrambi piccoli non è detto che sia un numero pure piccolo (detto in più rigorosi termini matematici: il rapporto tra due infinitesimi dello stesso ordine è un valore finito).
La figura successiva dovrebbe chiarire il concetto:

Negli studi statistici spesso non si può osservare tutta la popolazione, che può essere molto grande, o avere anche un numero infinito di individui (si pensi ai possibili risultati di un determinato esperimento che può teoricamente essere ripetuto infinite volte).
Pertanto il metodo che si seguirà sarà quello di osservare un campione, e dall'analisi statistica di esso si ricaveranno delle informazioni relative all'intera popolazione, attraverso il processo di inferenza statistica.
L'inferenza statistica quindi è quel processo, comprendente gli strumenti matematici necessari, che ci permette di passare dalle informazioni, osservate e misurate, e quindi note, sulla variabile statistica in un campione (ossia un sottoinsieme di individui) della popolazione, alla stima della distribuzione della variabile statistica all'interno dell'intera popolazione.
Il concetto di stima, nel suo significato generale, è il seguente: "Valutazione approssimata del valore numerico di una grandezza, e anche il valore numerico medesimo" (vocabolario Treccani, def. 3a).
Stimare il valore di un bene non significa esprimere il valore vero di quel bene, ma significa valutarlo, prevederlo. I questo significato è insito il fatto ceh una stima può essere più o meno buona. Se voglio vendere il mio orologio, e lo faccio stimare a un esperto, la stima che mi fornirà sarà più o meno vicina al valore cui effettivamente riuscirò a venderlo, seconda della sua capacità o bravura.
L'inferenza statistica, abbiamo detto, ci permette di effettuare una stima della distribuzione della variabile statistica all'interno dell'intera popolazione, in base all'osservazione di un campione della popolazione, e attraverso l'applicazione degli strumenti matematici che ci vengono forniti. Ci permetterà anche di dare un giudizio sul grado di attendibilità della stima stessa. E possiamo già capire che tanto sarà più grande il campione, quanto maggiore sarà l'attendibilità della stima.
L'esempio classico del lancio del dado permette di applicare questa semplice relazione matematica.
Qual'è la probabilità che se lancio un dado esca "6"?
I casi possibili sono 6: 1; 2; 3; 4; 5 e 6
I casi favorevoli sono quelli che hanno il risultato cercato, il "6", e sono solo 1
Quindi:
P= 1/6 =0,1666...
E poiché è un rapporto si può esprimere anche come percentuale:
P% = (q / n)·100
quindi, in questo caso:
P% = 16,66...%
La probabilità
esprime quindi la frequenza media con cui un evento
si verifica. Nel nostro caso l'evento "esce 6" si verifica mediamente
"1 volta su 6", o con la frequenza di 1/6, o del 16,66...%
Per informazione una distribuzione in cui la variabile statistica può avere solo due possiibili valori, come in questo caso: "maschi" o "femmine" (oppure "si" o "no", "vero" o "falso", "0" o "1"), prende il nome di distribuzione di Bernoulli.
Nell'esempio appena fatto la variabile statistica può assumere solo due valori: "maschio" o "femmina". Ma spesso la variabile statistica è continua, ha infiniti possibili valori: si pensi ad esempio all'altezza degli individui in una popolazione.
In questi casi, per fare delle stime su una popolazione, ci viene in aiuto la possibilità di prevedere ragionevolmente, in molti casi, come è fatta la distribuzione della variabile statistica all'interno della popolazione.
Si pensi all'esempio parlando della distribuzione limite. Se possiamo conoscere a priori la forma della distribuzione, saremmo certo aiutati nel nostro lavoro di applicare l'inferenza statistica.
E infatti lo studio della statistica mostra che le distribuzioni che descrivono molti fenomeni tendono ad assumere delle forme ben precise e riconoscibili.
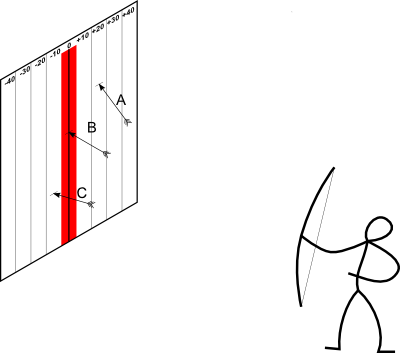

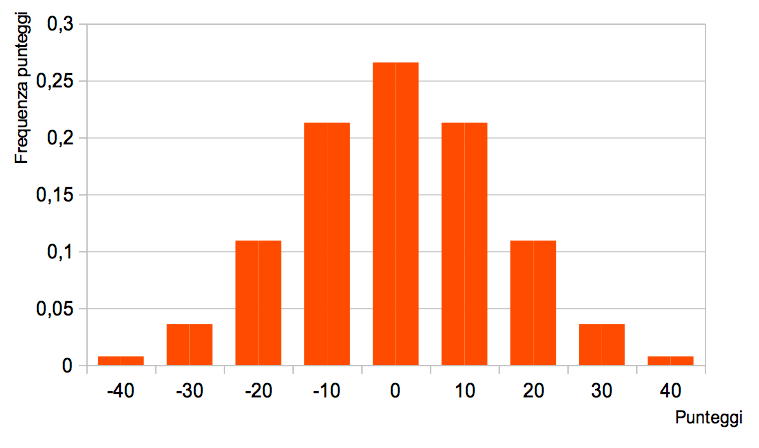
È evidente che più sarà bravo l'arciere, minore sarà la dispersione dell'istogramma.
All'aumentare del numero di lanci, come abbiamo visto, l'istogramma tenderà a una curva, che è la distribuzione limite.
Tale distribuzione ha la caratteristica forma "a campana", e questo fa pensare, per le caratteristiche che ha la variabile statistica (i risultati tendono ad avvicinarsi allo stesso risultato medio, i risultati sono influenzati da cause perturbanti, sia di segno positivo, sia di segno negativo, indipendenti e casuali) che la distribuzione dei risultati potrebbe seguire la distribuzione normale, o di Gauss.
Un altro esempio lo potremmo avere osservando come varia
un parametro misurato durante una produzione industriale.
Ad esempio, nella produzione di un lotto di determinato pezzo meccanico (ad esempio delle viti), la cui misura è prefissata (ad esempio il diametro), è del tutto normale che nella lavorazione avvengano degli imprecisioni piccole, indipendenti e casuali, che fanno sì che l'effettiva misura dei pezzi prodotti si distribuiscono spesso secondo la cosiddetta distribuzione normale o di Gauss: avremo in questo caso viti più sottili e viti più grosse, e la distribuzione del diametro delle viti avverrà secondo la distribuzione di Gauss.
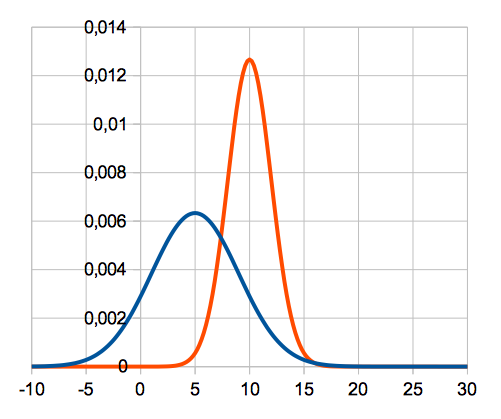
| media x | deviazione standard σ | |
| curva blu | 5 |
4 |
| curva arancione | 10 |
2 |
Ricordando che l'area sottesa da una curva di distribuzione limite tra due estremi rappresenta la frequenza di individui che hanno variabile statistica compresa tra i due limiti dell'area, osserviamo la figura che segue:
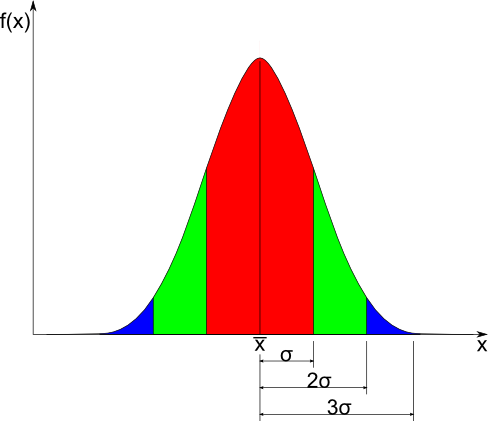
Si può dimostrare che, se la curva rappresenta una distribuzione di Gauss, l'area che va da una distanza pari alla deviazione standard σ a sinistra della media x, a una distanza paria alla deviazione standard a destra σ della media x (è la zona rappresentata in rosso) è circa il 68% dell'area sottesa da tutta la curva di Gauss (che va da -∞ a +∞);
l'area che va da una distanza pari a due volte (2·σ) la deviazione standard a sinistra della media x, a una distanza pari a due volte la deviazione standard (2·σ) a destra della media x (è la zona rappresentata in rosso più la zona rappresentata in verde) è circa il 95% dell'area sottesa da tutta la curva di Gauss;
l'area che va da una distanza pari a tre volte la deviazione standard (3·σ) a sinistra della media x, a una distanza pari a tre volte la deviazione standard (3·σ) a destra della media x (è la zona rappresentata in rosso più la zona rappresentata in verde più la zona rappresentata in blu) è circa il 99,7% dell'area sottesa da tutta la curva di Gauss.
In altre parole si può quindi affermare che:
A volte si chiama questa, per ricordarla facilmente, la "regola del 68-95-99"
La cosa è anche facilmente interpretabile come segue:
La terza fascia di confidenza contiene quasi tutti gli individui della popolazione. La probabilità del 99,7% è una probabilità quasi assoluta. In altre parole, al contrario, c'è una probabilità quasi nulla che un individuo non cada all'interno della terza fascia di confidenza.
Si vede quindi qual'è l'importanza della conoscenza della deviazione standard, in quanto ci permette di sapere quanti individui cadono all'interno di una certa fascia.
Poiché la curva della distribuzione di Gauss è simmetrica si possono anche fare altre semplici considerazioni su di essa, ad esempio:
e così via.
Si possono usare tavole per
calcolare la frequenza in una distribuzione di Gauss compresa anche
in fasce di ampiezza diversa σ, 2·σ e 3·σ.
Utilizzando un foglio di calcolo (come nelle applicazioni Libre Office, Open Office, Microsoft Excel etc.) è possibile utilizzare la funzione "=GAUSS(k)": il risultato sarà la percentuale compresa nella fascia tra [x] e [x + k·σ].
dove:
La miglior stima della media di una variabile della popolazione che segue una distribuzione normale è la media della stessa variabile del campione, che si calcola allo stesso modo. Ma quanto è buona questa stima? La stima della deviazione standard ce ne dà una significativa quantificazione.
È importantissimo anche stimare la deviazione standard di una popolazione che segue distribuzione di Gauss a partire dall'analisi di un campione. La regola non è così immediata come per la stima della media. Richiede infatti una piccola attenzione:
σc = √[∑(xi - x)2/(nc-1)]
dove:
È questa una distribuzione di grandissimo interesse per lo studio di quei fenomeni in cui avvengono una serie di eventi di un certo tipo, e l'istante (o la posizione) in cui avviene ciascun evento non è influenzato dall'istante (o dalla posizione) in cui avvengono gli altri eventi.
Se in un certo intervallo di tempo (o di spazio) il numero di eventi che si verificano varia in modo casuale, ma tuttavia questi eventi tendono ad avvenire mediamente sempre in un numero di volte costante, allora la distribuzione del numero di eventi tende a seguire la distribuzione di Poisson.
In altre parole la distribuzione di Poisson esprime la probabilità che degli eventi, il cui verificarsi non è influenzato dal verificarsi di un altro evento dello stesso tipo, avvengano un certo numero di volte in un certo intervallo di tempo (o di spazio).
Mentre la distribuzione di Gauss è "continua", nel senso che la variabile statistica può assumere infiniti valori reali (es: -5; 0,134444... etc.), la distribuzione di Poisson è "discreta" in quanto si applica a fenomeni per i quali è possibile effettuare un conteggio (0; 1; 2; 3...) del verificarsi degli eventi che caratterizzano il fenomeno stesso.
Anche la distribuzione di Poisson trova riscontro in moltissimi fenomeni
di tipo fisico, biologico, sociologico, logistico, e nello studio in
generale di svariati fenomeni dal punto di vista statistico.
Un primo esempio a cui possiamo pensare per capire i
concetti che sono sottesi alla distribuzione di Poisson potrebbe essere
dato dal numero delle nascite che avvengono nel reparto di maternità di un
certo ospedale in un certo intervallo di tempo.
Ogni nascita avviene in un certo istante e non è influenzata dal verificarsi delle altre nascite.
Se effettuiamo un conteggio delle nascite che si hanno in un certo intervallo di tempo, possiamo stimare il numero medio delle nascite in quell'ospedale in un uguale intervallo di tempo, o anche in intervalli di tempo differenti.
Se per esempio in una certa settimana contiamo 16 nascite, con questo dato a disposizione possiamo stimare che il numero medio settimanale delle nascite in quell'ospedale è di 16 nascite/settimana.
Ma siamo in grado di affermare che in tutte le settimane si avranno sempre 16 nascite?
Sicuramente no. Ma con il dato a disposizione, derivante da un conteggio di 16 nascite, è questa la miglior stima della numero medio di nascite che potremmo avere in una settimana.
È evidente che si potrebbe avere una stima ancora migliore, conteggiando
le nascite in un intervallo di tempo più lungo, e quindi verosimilmente
ottenendo un conteggio più grande, ma con quel dato a disposizione è
questa la miglior stima possibile.
Il conteggio effettuato in un certo intervallo di tempo rappresenta quindi la miglior stima del numero medio di eventi nell'intervallo considerato del fenomeno studiato.
Se contiamo 16 nascite/settimana possiamo dire che il numero più probabile di nascite che si hanno in una settimana è 16, e che ci sarà una probabilità via via inferiore che le nascite si discostino, in più o in meno, dal valore medio stimato 16.
Simbolicamente possiamo scrivere:
La distribuzione di Poisson ha equazione:
P(k) = (νk / k!) · e-ν
agli studenti
di OPP non è richiesto memorizzare questa equazione, ma è importante
comunque notare quanto segue:
che esprime la probabilità P(k) che si verifichi un certo numero di eventi k nell'intervallo considerato in funzione del conteggio effettuato.
È utile rappresentarla graficamente (a partire dal valore del conteggio ν = 16 dell'esempio fatto):
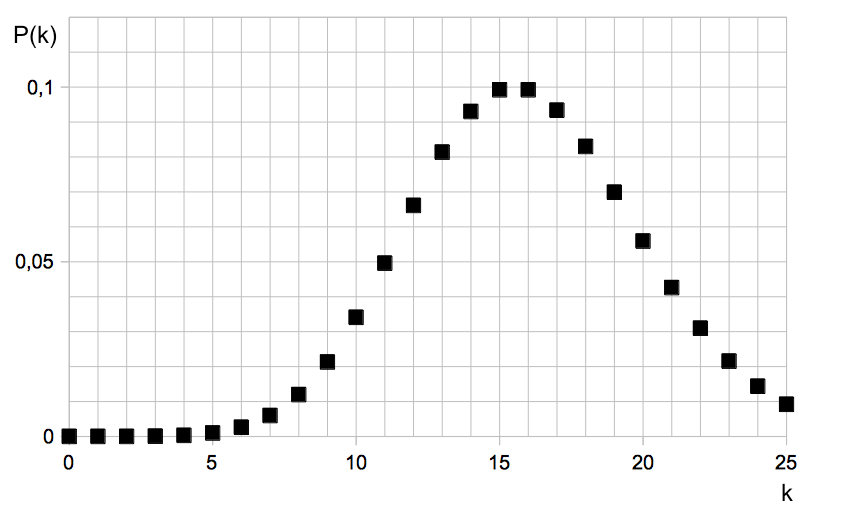
Si noti che la distribuzione è stata tracciata "a punti", e non con una linea continua, ad evidenziarne la natura discreta (e non continua) della variabile statistica, che rappresenta il numero di eventi che si potrebbero verificare.
Si noti anche che, in questo esempio, la probabilità massima si ha per un numero di 16 nascite/settimana, e che tale probabilità è 0,0992 (o 9,92% se espressa come probabilità percentuale), e che man mano che ci allontaniamo, in più o in meno, dal numero medio, la probabilità tende a diminuire. È assai poco probabile, ma non impossibile, che avvengano, ad esempio, solo 5 nascite a settimana.
Anche per la distribuzione di Poisson è importante conoscere la deviazione standard, in quanto ci dà un informazione importante su come sono distribuite le probabilità dei vari numeri di eventi.La statistica mostra come per la distribuzione di Poisson, la deviazione standard del numero di eventi possa venire stimata dalla radice quadrata del conteggio effettuato:
√ν = miglior stima di σ
dove:
Inoltre, quando il conteggio dà un valore abbastanza elevato (un conteggio di almeno 10 eventi è in genere considerato un valore abbastanza elevato), la distribuzione di Gauss approssima molto bene la distribuzione di Poisson, e pertanto alcune proprietà della distribuzione di Gauss potranno essere applicate a quella di Poisson. In particolare la "regola del 68-95-99%" (e non a caso la forma del grafico della distribuzione di Poisson assomiglia a quella del grafico della distribuzione di Gauss).
In pratica nell'esempio fatto, se 16 sono le nascite conteggiate in una settimana, possiamo affermare che:
ν = 16 è la media stimata delle nascite settimanali
σ = √ν = √16 = 4 è la deviazione standard stimata.
applicando la regola del 68-95-99% possiamo individuare le fasce di confidenza e affermare che:
In pratica saranno assai improbabili le settimane in cui si avranno meno di 4 o più di 28 nascite. E in genere è proprio questo il dato che interessa maggiormente: quante nascite al massimo si possono avere in una settimana (salvo quel rarissimo 0,15% di casi che cadono a destra della terza fascia di confidenza).
Avendo stimato una media di 16 nascite stimate, potremmo esprimere questo dato anche come numero di nascite medie mensile (di 30 giorni) nm semplicemente facendo una proporzione:
Non ci si stupisca di avere un numero non intero! Il conteggio è sempre un numero intero, ma il conteggio è stato effettuato, in questo caso, in un intervallo di una settimana, e da lì abbiamo calcolato, con una proporzione, il numero medio mensile.
E si faccia anche attenzione a non calcolare la deviazione standard a partire dalla media mensile! La deviazione standard va sempre calcolata facendo la radice quadrata del conteggio effettuato, e sarà la deviazione standard rispetto all'intervallo in cui è stato effettuato il conteggio, ossia la settimana. Se vogliamo conoscere le fasce di confidenza rispetto alla media mensile, dobbiamo fare analoga proporzione
Quindi:
Non si verificheranno quasi mai lotti in cui si avranno più di 40 pezzi difettosi ogni 1˙000.
Anche questo risultato si può estendere, facendo una proporzione, a lotti di un numero differente a 1˙000 pezzi. Ad esempio, poiché non si hanno mai più di 40 pezzi difettosi ogni 1˙000, si può affermare che in un lotto di 5˙000 pezzi non si avranno quasi mai più di 200 pezzi difettosi.
Analizzando la produzione di queste viti (o analizzandole tutti, o applicando l'inferenza statistica a uno o più campioni), si può affermare che:
Con il termine di tolleranza si esprime l'errore massimo consentito dell'intera produzione.
È chiaro che:
Poiché è evidentemente più costoso garantire tolleranze strette, la scelta della tolleranza dipenderà dalle esigenze di precisione: se le nostre viti devono essere utilizzate in costruzioni meccaniche di precisione sarà necessarie viti realizzate con tolleranze strette. Ma se non si ha questa esigenza è inutile utilizzare lavorazioni più precise, e quindi più costose.
Per analizzare se una produzione garantisce la tolleranza richiesta ci torna utile l'analisi statistica e, posto che di una produzione si possa affermare che segue la distribuzione di Gauss, si potrà valutare se il parametro controllato rientra nelle fasce di confidenza, così come le abbiamo definite descrivendo la distribuzione di Gauss.
Il valore nominale e la tolleranza possono essere indicato come segue:
x = xnom ± ∆x
dove:
Parlando dell'esempio della lunghezza delle viti potrebbe essere presentata così:
L = 20 ± 0,1 mm
che si significa che le viti hanno una lunghezza nominale di 20 mm,
e una tolleranza ammessa, in più o in meno, di 0,1 mm.
Saranno ammesse viti lunghe tra 19,9 mm e 20,1 mm.
La fascia o intervallo di tolleranza è l'intervallo compreso tra [xnom - ∆x] e [xnom + ∆x]. Nel nostro esempio tra 19,9 mm e 20,1 mm.
Si noti che il valore nominale e a tolleranza sono indicati con la stessa unità di misura. Si può però indicare la tolleranza come tolleranza percentuale, così:
x = xnom ± ∆%x
dove:
Nel nostro esempio sarebbe indicato così:
L = 20 mm ± 0,5%
in quanto lo 0,5% di 20 mm è 0,1 mm.
Si osservi la posizione delle unità di misura (e del simbolo %) nella presentazione del parametro nei due esempi fatti!
A volte si utilizza anche il simbolo ‰, che ha il significato di "per mille". Il nostro esempio diventerebbe:
L = 20 mm ± 5‰
Applichiamo le proprietà della distribuzione di Gauss a un problema applicabile nella produzione di uno stampato.
Come è noto un parametro che lo stampatore deve tenere sotto costante controllo durante la tiratura, nel processo di stampa lito-offset, è la costanza dello spessore dell'inchiostro. Ci sono varie cause che influenzano lo spessore dell'inchiostro, la più comune delle quali è sicuramente la temperatura. Col procedere della tiratura, ad esempio, l'attrito esercitato dai rulli inchiostratori tende a scaldare leggermente l'inchiostro aumentandone la fluidità, e quindi a facilitarne la discesa sulla forma da stampa. Lo stampatore potrà intervenire intervenendo sulla regolazione del calamaio. Ma altre cause non sono sempre facilmente indagabili e individuabili.
Possiamo ipotizzare ragionevolmente che, poiché la variabilità dello spessore dell'inchiostro è influenzata da tante cause perturbanti piccole, indipendenti e casuali, che essa segua la distribuzione di Gauss.
Ma misurare direttamente lo spessore dell'inchiostro sarebbe praticamente impossibile, per cui il parametro che viene misurato è in realtà la densità ottica dell'inchiostro sulla "tacca del pieno" della scala di controllo, mediante il densitometro, poiché densità e spessore dell'inchiostro sono pressoché proporzionali.
Ricordiamo che la densità ottica (d'ora in poi la chiamiamo semplicemente densità) è data da:
D = log (Φi/Φr)
dove:
e che quindi, essendo il logaritmo di un rapporto
tra due grandezze omogenee (che hanno entrambe la stessa unità di misura),
è una grandezza che non ha unità di misura. Se
fosse necessario rinfrescarsi sul concetto di densità le idee si veda >>
qui.

Una scala di controllo per stampa lito-offset in quadricromia. Il controllo dello spessore di inchiostro viene effettuato misurando la densità delle "tacche del pieno", ossia dove si ha 100% di percentuale di punto di ogni inchiostro da solo (non sovrastampato agli altri). In questo caso sulle tacche contrassegnate con la sola lettera K, C, M, Y rispettivamente
E' fondamentale mantenere il valore della densità che deve essere quanto più prossimo possibile al valore della densità ottimale, allo scopo di mantenere il più alto possibile contrasto di stampa e quindi la corretta colorimetria dello stampato. Ragionando ad esempio sull'inchiostro nero (ma il concetto è lo stesso anche per gli altri colori), un valore di densità in difetto rispetto al valore ottimale porterebbe ad avere neri sbiaditi, mentre un valore di densità in eccesso rispetto al valore ottimale (quindi una quantità di inchiostro eccessiva), porterebbe ad avere grigi scuri "impastati", ossia in cui non sarebbero distinguibili i diversi valori tonali nelle zone più scure delle immagini.
Si vede quindi che, aprendo il calamaio, e aumentando quindi progressivamente la quantità di inchiostro, e quindi la densità, il contrasto di stampa dapprima aumenta, e poi diminuisce. Il valore di densità che si ha quando il contrasto di stampa è massimo è il valore di densità ottimale.
Il valore di densità ottimale viene ricavato mediante prove preliminari, e dipende anzitutto dal tipo di carta utilizzato.
Indicativamente, per il nero, e per una carta patinata lucida, la densità ottimale potrebbe essere attorno al valore 1,80
Sempre per il nero, per una carta usomano, potremmo avere un valore ottimale attorno al valore 1,40.
A seconda delle caratteristiche di qualità richieste allo stampato è ammessa una tolleranza più o meno piccola rispetto a tale valore ottimale.
Ad esempio la densità richiesta potrà essere espressa in questa forma:
che significa che la densità dovrà essere sempre compresa tra 1,75 e 1,85.
Non è ovviamente possibile misurare la densità su tutti i fogli della tiratura, per cui lo stampatore estrarrà un foglio campione a intervalli regolari (ad esempio un foglio ogni 1000 fogli stampati) e su questo effettuerà la misura della densità.
Il problema che ci si pone qui è se, a partire da una serie di misure effettuate, si è in grado di affermare che ragionevolmente nessun foglio della tiratura eccederà i valori ammessi.
Supponiamo quindi che per lo stampato che stiamo realizzando, in una tiratura di 6000 fogli, si debba avere un valore di densità richiesta pari a 1,80 ± 0,05
Supponiamo che lo stampatore effettui una misura della densità del nero sulla scala di controllo ogni 1000 fogli. Estrarrà quindi il 1000°, il 2000°, il 3000°, il 4000° e il 5000° foglio. Effettua la misura dunque su un campione di 5 fogli.
E che rilevi i seguenti valori di densità:
Ci si chiede se a partire da questi dati siamo in grado di dire che nessun foglio è al di fuori dei valori ammessi.
Un errore grossolano potrebbe essere quello di pensare che, poiché tutti i valori del campione sono all'interno della fascia di tolleranza, ossia sono tutti valori ammessi, allora anche tutta la tiratura lo sarà. Ma attenzione: stiamo ragionando su solo 5 fogli! Quel valore 1,76 è piuttosto vicino al limite che è 1,75. Potrebbe darsi il caso che in alcuni fogli, tra quelli che non fanno parte del campione, il valore di densità venga superato.
Se ipotizziamo che la variabilità della densità segua la distribuzione di Gauss, possiamo rispondere a questa domanda cominciando a stimare la densità media della tiratura. Come abbiamo visto la miglior stima, con il campione a disposizione, di 5 fogli, è data dalla media del campione stesso, ed è pari a:D = (∑Di)/n = (1,81 + 1,76 + 1,79 + 1,78 + 1,81)/5 = 1,79
calcoliamo poi la deviazione standard del campione:
σc = √[∑(Di - D)2/(nc-1)]
= √[(1,81 - 1,79)2 + (1,76 - 1,79)2 + (1,79 -
1,79)2 + (1,78 - 1,79)2 + (1,81 - 1,79)2/(5-1)]
= 0,0212132034 ≈ 0,02 (arrotondando il valore finale al secondo decimale)
Applicando la regola vista (la regola del 68-95-99%) la conoscenza di questo valore ci permette ragionevolmente di affermare che:
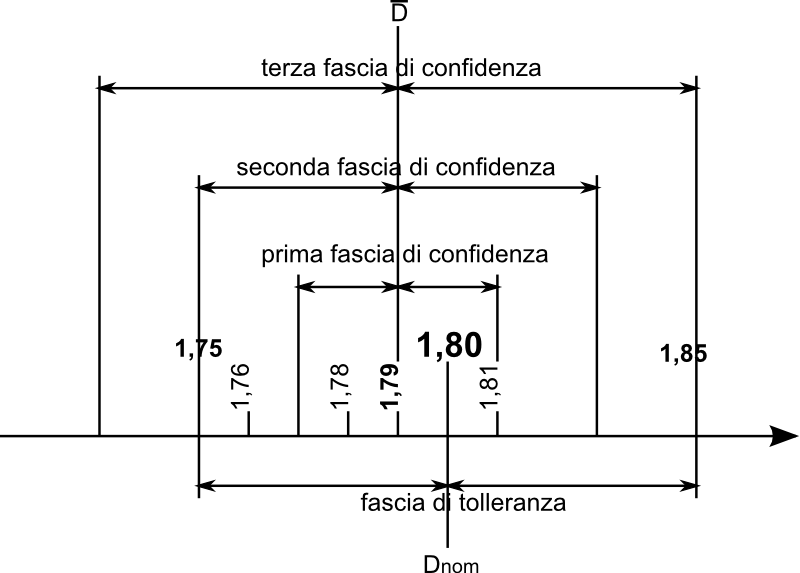
La fascia di tolleranza è centrata sul valore nominale (Dnom), mentre le fasce di confidenza sono centrate sul valore medio stimato (D). Si vede che, poiché quasi tutta la produzione (il 99,7%) è compresa nella terza fascia di confidenza, ci sarà una certa percentuale della produzione che cade fuori dalla fascia di tolleranza, e quindi non è ammissibile.
E' interessante quindi osservare che, nonostante tutti i valori di densità rilevati dal campione siano all'interno dell'intervallo di ammissibilità, applicando correttamente i concetti dell'inferenza statistica, siamo in grado di affermare che probabilisticamente ben il 2,5% dei fogli (una quantità non trascurabile, nel caso in esame si tratta del 2,5% di 6000 fogli, ossia di ben 150 fogli) avrà densità inferiore a 1,75.
Mentre nel caso precedente abbiamo applicato il concetto di tolleranza ponendoci in un'ottica di qualità di prodotto, in questo caso ci poniamo invece in un'ottica di qualità di processo.
Ossia nell'esempio precedente abbiamo valutato che il prodotto si mantenesse entro i parametri qualitativi richiesti, qui invece valutiamo un aspetto relativo alla qualità del processo.
Ad esempio la quantità di scarti di lavorazione rappresenta un importante parametro qualitativo del processo. È tuttavia evidente che qualità di processo e qualità di prodotto siano due aspetti tra i quali esiste un'importante correlazione.
Applichiamo le proprietà della distribuzione di Poisson a un problema applicabile nella produzione di uno stampato, relativamente agli scarti di tiratura.
Lo scarto di tiratura è un evento impossibile da eliminare completamente e deve essere conosciuto e quantificato. In pratica se il cliente chiede una tiratura, ad esempio, di 10.000 copie, siamo sempre costretti a preventivare un numero maggiore di fogli rispetto a quelli strettamente necessari in assenza di scarto, in quanto l'esperienza mostra che un certo numero di scarti affligge qualsiasi tiratura.
E poiché lo scarto è una voce di costo piuttosto importante, sarà necessario stimarlo nella maniera più esatta possibile:
Limitando per semplicità qui il ragionamento allo scarto di tiratura (non considerando quindi altri scarti di produzione, come lo scarto di piegatura), e pensando che la tipica causa di scarto in tiratura è il foglio "inceppato", ipotizziamo di contare, ad esempio:
ν = 16 fogli inceppati ogni 1˙000 fogli introdotti
Possiamo dire che la deviazione standard è:
σ = √16 = 4 fogli inceppati ogni 1˙000 fogli introdotti, che, applicando la solita regola del 68-95-99%, significa che:
Possiamo dire che, per tutte le tirature di 1˙000 fogli, non si avranno quasi mai più di 28 fogli inceppati.
Ma è utile stimare le quantità di fogli inceppati in termini percentuali, cosicché il dato potrà essere utilizzato quale che sia la tiratura.
Poiché il dato trovato è di 28 fogli su una tiratura di 1˙000, questi corrispondono a una percentuale di:
28/1000 = 0,028 = 2,8% che sarà la miglior stima della percentuale massima di inceppamenti in una generica tiratura.
In altre parole c'è meno dello 0,15% di probabilità (una probabilità assai rara) che in una tiratura generica si inceppino più del 2,8% di fogli.
Applicando questo dato a una tiratura, ad esempio, di 40˙000 fogli, possiamo stimare uno scarto massimo del 2,8% di 40˙000, ossia:
40˙000 · 2,8/100 = 1˙120 fogli
Aumentando l'ampiezza dell'osservazione (ad esempio effettuando il conteggio su 5˙000 fogli anziché su 1˙000), miglioreremmo certo la bontà della stima. E' però anche evidente che non sempre, nella pratica operativa, è possibile o conveniente effettuare delle osservazioni molto lunghe, e quindi ci si dovrà accontentare di stime con un certo livello di incertezza.
:: Torna all'indice di Organizzazione e gestione dei processi produttivi ::
