"In senso concreto, il luogo dove avvengono le contrattazioni per la vendita e l’acquisto di determinati prodotti e dove normalmente si incontrano, tutti i giorni, o in giornate stabilite, compratori, venditori e intermediari per effettuare transazioni commerciali relative a merci varie o anche a una sola merce. Per estensione, l’insieme degli operatori legati tra loro in determinati rapporti d’affari o, sotto altro aspetto, l’insieme delle operazioni relative a un determinato bene o gruppo di beni" (definizione tratta da Enciclopedia Treccani on-line www.treccani.it/enciclopedia/mercato/).
In altre parole: il luogo (inteso come ambito) dove si incontrano la domanda e l'offerta.
Ma si può estendere il concetto di mercato non solo ai beni, ma anche ai servizi.
Esempi: il mercato cartario (beni), il mercato dei trasporti (servizi).
In economia classica (Adam Smith - Scozia: 1723-1790 e David Ricardo - Inghilterra: 1772-1823) si considerano i tre fattori della produzione:
Si può estendere il concetto di "terra" a ciò che è destinato a essere trasformato: la materia prima e il concetto di "capitale" a ciò che si utilizza per trasformare la materia prima in prodotto: i beni strumentali. Per "lavoro" si intende il lavoro umano, sia manuale che intellettuale.
I fattori della produzione concorrono alla produzione dei beni e dei servizi.
Un processo produttivo porta pertanto a trasformare la materia prima in prodotto attraverso l'utilizzo (diretto o indiretto) dei beni strumentali.
In senso letterale è: "Tutto ciò che la terra produce o che costituisce il risultato di un’attività umana" (definizione tratta da Enciclopedia Treccani on-line www.treccani.it/enciclopedia/prodotto/)
Più specificamente, in economia, è ciò che deriva da un'attività produttiva: un bene o un servizio ottenuto dalla trasformazione di altri beni o servizi
Il Codice civile, all'art. 810 definisce il bene così: "Sono beni le cose che possono formare oggetto di diritti".
Un servizio è invece il "risultato di ogni attività svolta dall’uomo direttamente attraverso il proprio lavoro, oppure indirettamente, attraverso beni economici, allo scopo di soddisfare propri bisogni" (definizione tratta da Enciclopedia Treccani on-line: http://www.treccani.it/enciclopedia/servizio).
I beni possono essere materiali (ad esempio un edificio, un automezzo), o immateriali (ad esempio un brevetto).
I servizi hanno sempre natura immateriale, ossia si esauriscono nel momento in cui vengono realizzati (ad esempio una consulenza,un trasporto).
In senso letterale è: "ogni materia fornita dalla natura e base di successive lavorazioni" (definizione tratta da Enciclopedia Treccani on-line: http://www.treccani.it/enciclopedia/materia)
Più specificamente, in economia, è ogni materia o elemento di cui ci si serve per produrre, anche se a sua volta è derivante da un altra attività produttiva (ossia è a sua volta un prodotto).
Ciò che è prodotto per una attività produttiva, potrebbe essere materia prima per un'altra.
Ad esempio: la carta è il prodotto dell'industria grafica, ma è la materia prima dell'industria della stampa
Sono quei beni (materiali e immateriali) che hanno la funzione, mediante il loro utilizzo continuativo, di concorrere al profitto di un impresa, senza tradursi in denaro attraverso la vendita. Sono detti anche cespiti. Possiamo in certi casi chiamarli anche attrezzature.
Esempi:
Beni strumentali e materie prime, assieme, costituiscono i mezzi della produzione.
Il lavoro pertanto agisce sui mezzi della produzione,
utilizzando i beni strumentali e trasformando con essi,
direttamente o indirettamente, le materie prime.
L'impresa è l'attività esercitata dall'imprenditore. Questi è definito dal codice civile (art. 2082) come: "chi esercita professionalmente un'attività economica organizzata al fine della produzione o dello scambio di beni o di servizi". E' un concetto giuridico.
L'azienda è l'insieme dei mezzi (immobili, attrezzature, personale, metodi, procedure...) con cui viene esercitata l'attività di impresa. E' un concetto economico.
La ditta è la denominazione commerciale (e l'eventuale logo) dell'impresa.
La società è una specifica tipologia di impresa: è un soggetto giuridico esercente attività di impresa. Il codice civile (art. 2247), stabilisce che "con il contratto di società due o più persone conferiscono beni o servizi per l'esercizio in comune di un'attività economica, allo scopo di dividerne gli utili"
L'utile è l'eccedenza dei ricavi sui costi che si ottiene da un'attività di impresa.
In pratica:
UTILE = RICAVI - COSTI
Attenzione pertanto a non confondere i costi con gli utili!
Il prezzo è il valore economico di un singolo prodotto (bene o servizio).
Il ricavo che consegue dalla vendita di una certa quantità di prodotti è dato da:
RICAVO = PREZZO DEL SINGOLO PRODOTTO * QUANTITA' DI PRODOTTI VENDUTI
I costi di produzione sono dati dalla somma dei costi fissi e dei costi variabili.
COSTI DI PRODUZIONE = COSTI FISSI + COSTI VARIABILI
Questi costi si riferiscono all'intera produzione. Se invece li riferiamo a un singolo prodotto abbiamo:
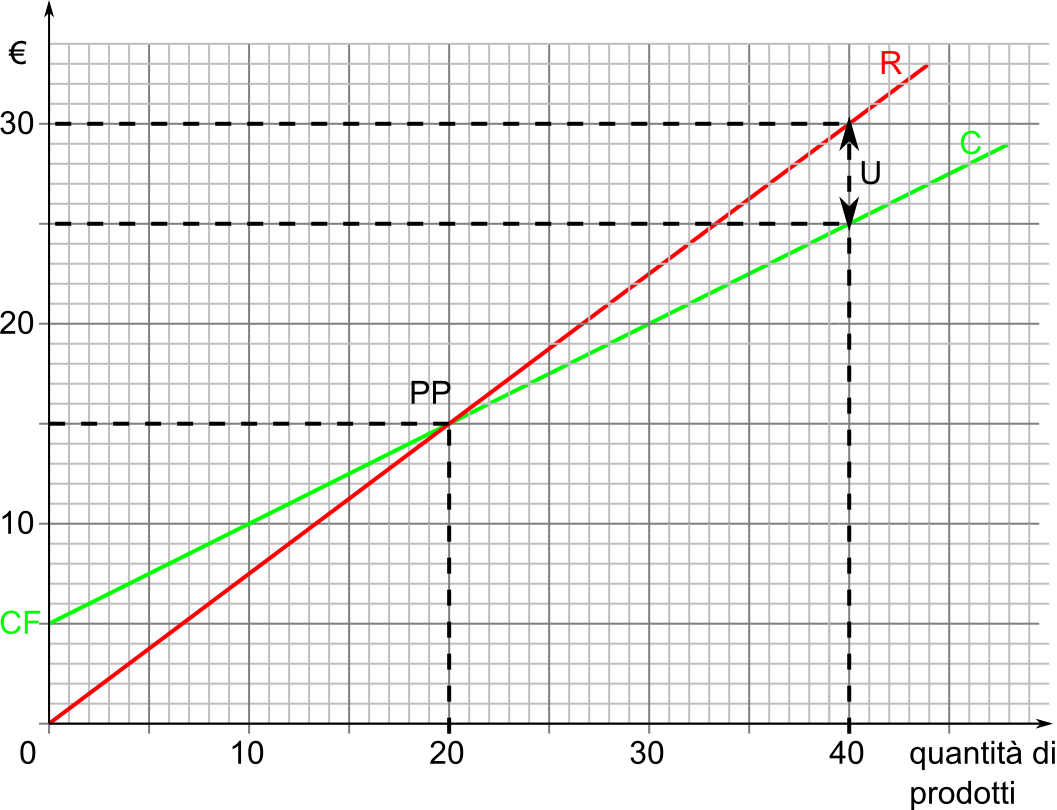
Il pareggio rappresenta la situazione in cui i ricavi coprono tutti
i costi della produzione (costi fissi e costi variabili).
Trovare il punto di pareggio significherà pertanto trovare la quantità di singoli prodotti che sarà necessario produrre e vendere affinché i ricavi coprano tutti i costi della produzione (costi fissi e costi variabili).
E' evidente che al punto di pareggio l'utile sarà zero.
In inglese viene chiamato anche break even point.
Il signor Citroni decide di produrre e vendere spremute di arancia.
Compra delle arance, dei bicchieri di carta usa-e-getta e uno spremiagrumi.
Decide che ogni spremuta sarà fatta con due arance.
Paga lo spremiagrumi 5 euro.
Paga le arance 20 centesimi di euro l'una. Usiamo i decimali: 0,20€ l'una.
Paga i bicchieri di carta usa-e-getta 10 centesimi di euro l'uno. Usiamo i decimali: 0,10€ l'uno.
Il signor Citroni decide di vendere le spremute a 0,75€.
Proviamo a rispondere alle seguenti domande:
Supponiamo che il signor Citroni produca e venda 40 spremute, utilizzando tutte le arance e i bicchieri che ha acquistato:
Supponiamo invece che il signor Citroni produca e venda 80 spremute, utilizzando tutte le arance e i bicchieri che ha acquistato:
E supponiamo ora che il signor Citroni, visto il grande successo delle sue spremute che tutto il quartiere desidera, decida di venderle a 2€ l'una, e ne produca 100, e siccome sono così buone, riesca a venderle tutte lo stesso. In questo caso:
Scriviamo in forma simbolica i concetti visti:
U: utileU = R - C
C = CF + CV
CV = ∑CM
Nell'ipotesi fatta, particolarmente semplice, i costi marginali si mantengono costanti (ossia Citroni paga le arance e i bicchieri sempre lo stesso, indipendentemente da quanti ne compra), quindi sarà:
CV = CM*Qp
Anche il prezzo è costante, nel senso che il prezzo rimane lo stesso
indipendentemente da quante spremute vengono vendute.
R = P*Qv
e sostituendo la terza nella seconda abbiamo:
C = CM*Qp + CF
e a sua volta sostituendo questa, e la quarta, nella prima avremo:
U = P*Qv - CM*Qp - CF
e, nell'ipotesi particolare, ma molto più semplice da analizzare, in cui tutti i prodotti effettivamente prodotti verranno venduti, sarà:
Qp = Qv
chiamiamo allora Q la quantità di prodotti sia realizzati sia venduti:
Q = Qp=Qv
possiamo scrivere, raccogliendo q:
U = (P - CM)*Q - CF
che è una relazione molto comoda da utilizzare. La si legga attentamente dando ad ogni simbolo il suo corretto significato!
Essa consente di trovare quanto vale l'utile, una volta che è
stato assegnato il prezzo di vendita del singolo prodotto, ed è
nota la quantità di prodotti realizzati e venduti, il costo
fisso e il costo marginale.
Le precedenti relazioni possono inoltre, per esempio, essere utilizzate per trovare il punto di pareggio.
Ricordiamo infatti che abbiamo definito il pareggio come la situazione in cui i ricavi coprono tutti i costi della produzione (costi fissi e costi variabili) e che il punto di pareggio rappresenta la quantità di singoli prodotti che sarà necessario produrre e vendere affinché i ricavi coprano tutti i costi della produzione, e che pertanto al punto di pareggio l'utile è pari a zero.
Possiamo allora scrivere la precedente relazione, in cui tutti i prodotti realizzati venivano venduti, ponendo U = 0:
0 = (P - CM)*Q - CF
che, risolvendola rispetto a Q, che ora è un'incognita, e potremmo chiamarla "la quantità che mi dà il punto di pareggio" Qpp, e dà:
Q = Qpp = CF/(P - CM)
| q |
CF |
CM |
CV |
C |
P |
R |
U |
| 0 |
5 |
0,50 |
0 |
5 |
0,75 |
0 |
-5 |
| 1 |
5 |
0,50 |
0,50 |
5,50 |
0,75 |
0,75 |
-4,75 |
| 2 |
5 |
0,50 |
1 |
6 |
0,75 |
1,50 |
-4,50 |
| ... |
... |
... |
... |
... |
... |
... |
... |
| 19 |
5 |
0,50 |
9,50 |
14,50 |
0,75 |
14,25 |
-0,25 |
| 20 |
5 |
0,50 |
10 |
15 |
0,75 |
15 |
0 |
| 21 |
5 |
0,50 |
10,50 |
15,50 |
0,75 |
15,75 |
0,25 |
| ... |
... |
... |
... |
... |
... |
... |
... |
| 40 |
5 |
0,50 |
20 |
25 |
0,75 |
30 |
5 |
Ricordiamo che nel piano cartesiano la pendenza di una linea è data dal rapporto tra l'incremento delle ordinate e quello delle ascisse. Se la pendenza è costante allora quella linea è una retta.
È poi possibile definire il costo fisso unitario, come:
CFU = CF /Qp
dove si vede che all'aumentare della
quantità di prodotti realizzati, il CFU tende a zero.
Il Costo unitario invece sarà:
CU = C/Qp
e quindi sarà:
CU = CFU + CVU
Ma CVU, il costo variabile unitario, nel caso che il costo marginale sia costante, coincide con il costo marginale stesso, per cui:
CU = CF/Qp + CM
dove si vede che all'aumentare della quantità di prodotti realizzati, il CU tenderà a eguagliare il costo marginale.
Potremo comunque rifare i ragionamenti visti prima parlando di costi (fissi e variabili) annuali, di ricavi annuali, di utili annuali e, ancora, di quantità prodotte e/o venute annualmente.
Abbiamo fin qui identificato i costi variabili con il costo delle materie prime, ma in genere ci sono anche altri costi variabili: per esempio il signor Citroni è imprenditore di se stesso, non ha dovuto sostenere dei costi del lavoro, e il costo del lavoro può essere sia un costo fisso, sia un costo variabile. Discuteremo questo aspetto più avanti.
Abbiamo fatto anche l'ipotesi che il costo marginale sia sempre lo stesso, indipendentemente da quante materie prime vengono acquistate, ma anche in questo caso non è sempre così: acquistandone molte si potranno ottenere dai fornitori di aranche dei prezzi delle stesse inferiori, facendo così delle economie di scala.
Ma potrebbe anche darsi il caso che, se la domanda di prodotti aumentasse di molto, la produzione dovrebbe adeguarsi, e potrebbe diventare meno efficiente, per lo meno nel breve periodo. Nel nostro semplice esempio, potrebbe darsi il caso che se il signor Citroni dovesse produrre 24 ore al giorno, sarebbe costretto ad assumere un aiutante, e pagarlo. Potrebbe essere necessario fare nuovi investimenti (ad esempio uno spremiagrumi elettrico, più produttivo) per risucire a soddisfare la domanda, ma questo avverrò solo nel lungo periodo.
Abbiamo poi fatto l'ipotesi che tutte le materie prime diventassero prodotti, e che tutti i prodotti venissero venduti, ma non è sempre così, ovviamente, ci sarà dell'invenduto, e questo ovviamente costituisce un mancato ricavo, quindi a sua volta un costo.
Infine abbiamo lasciato che il signor Citroni stabilisse liberamente il prezzo, ma ovviamente sarà in questo vincolato dalle condizioni del mercato.
Analizzare i costi della produzione è quindi ovviamente più complesso, ma i concetti utilizzati qui continueranno a tornarci comodi.
Appare subito evidente che il costo delle
materie prime rappresenta un costo variabile. Infatti quante più unità
di prodotto dobbiamo produrre, quante più materie prime dobbiamo
acquistare, quindi i costi delle materie prime rientriano nella
definizione di costo variabile: costi che dipendono dalla quantità
prodotta.
Abbiamo qui identificato i costi variabili con il costo delle materie prime, e il costo fisso con il costo dei beni strumentali, ma non abbiamo considerato il costo del lavoro.
Il costo del lavoro può essere, a seconda dei casi, un costo fisso, o un costo variabile. Per sapere di che tipo di costo si tratta, si pensi sempre alle definizioni di costi fissi e di costi variabili.
Quando il costo del lavoro non dipende dalla quantità di prodotti realizzati, è un costo fisso. Tale è il caso del costo relativo alle retribuzioni fisse dei dipendenti. Qualora ad esempio, per qualsiasi motivo, la produzione diminuisse, quel costo non cambierà.
Quando il costo del lavoro dipende dalla quantità di prodotti realizzati, è un costo variabile. Tele è il caso ad esempio del costo relativo alle retribuzione dei lavoratori assunti "a chiamata", o interinali, o pagati a cottimo, o ancora dei dipendenti quando chiamati a svolgere lavoro straordinario per coprire ad esempio dei picchi di produzione in determinati periodi. Chiaro che questo lavoro, avendo un costo solo quando la produzione aumenta, è un costo variabile.
Un bene strumentale ha in genere una vita utile produttiva che si protrae per più di una sola annualità.
Per ammortamento si intende un procedimento contabile con cui si ripartisce il costo di un bene strumentale sul numero di anni di presumibile utilizzo del bene strumentale stesso.
In pratica, ad esempio, se un bene strumentale ha una vita utile produttiva prevista di 10 anni, nel bilancio aziendale il costo di acquisto di quel bene non graverà per intero soltanto nel bilancio dell'anno in cui il bene è stato acquistato, ma graverà soltanto per un decimo del suo costo nei 10 anni consecutivi a partire da quello dell'acquisto.
In altre parole in ciascun bilancio annuale comparirà la quota annua di ammortamento, ossia:
QUOTA ANNUA AMMORTAMENTO = COSTO ACQUISTO DEL BENE STRUMENTALE / ANNI DI VITA PRODUTTIVA PREVISTA DEL BENE STRUMENTALE
La quota annua di ammortamento è quindi, evidentemente, un costo fisso.
Il Decreto del Presidente della Repubblica 22 dicembre 1986, n. 917 "Approvazione del testo unico delle imposte sui redditi" (brevemente DPR 917/86: TUIR) e successive modificazioni, all'art. 102 ("Ammortamento dei beni materiali" ), comma 1, stabilisce che: "Le quote di ammortamento del costo dei beni materiali strumentali per l'esercizio dell'impresa sono deducibili a partire dall'esercizio di entrata in funzione del bene".
In pratica la quota annua di ammortamento, rientrando tra i costi di produzione, viene sottratta ai ricavi e va in diminuzione degli utili, con conseguente beneficio dal punto di vista fiscale. L'IRES, l'imposta sui redditi delle società, è calcolata infatti a partire dagli utili (attualmente, anno 2019, in una percentuale del 24%).Nel nostro esempio abbiamo fatto l'ipotesi che il costo marginale fosse sempre lo stesso, indipendentemente da quante materie prime vengono acquistate, ma anche in questo caso non è sempre così: acquistandone molte si potranno ottenere dei prezzi delle stesse inferiori, facendo così delle economie di scala.
Oppure, poiché spesso la produzione industriale comporta degli scarti, ossia non tutte le materie prime diventano prodotto, è comunque in genere vero che al crescere della produzione gli scarti tendono percentualmente a diminuire.
Possiamo definire le economie di scala come quelle economie legate a quei costi marginali che diminiscono all'aumentare della quantità prodotta.
In pratica quella che è stata rappresentata nel precedente grafico come la retta dei costi, con pendenza quindi costante, diventerebbe ora una curva che, pur sempre crescente, avrebbe la pendenza che man mano diminuisce al crescere della quantità di prodotti realizzati, quindi con concavità diretta verso il basso.
A causa delle economie di scala quindi il costo aggiuntivo per produrre le unità aggiuntive sarà inferiore di quello per produrre le precedenti. Riguardando la definizione di costo marginale si capisce che il costo marginale, grazie alle economie di scala, tende a diminuire.

Ci può essere (e in genere c'è) anche il caso in cui, quando la produzione deve crescere molto, perché c'è un aumento della domanda, essa possa diventare meno efficiente e le unità di prodotto aggiuntive costeranno un poco più delle precedenti. Ad esempio: sarà necessario retribuire i lavoratori per il lavoro straordinario (il costo orario del lavoro straordinario è maggiore).
I costi marginali, quindi, a un certo punto, cominceranno allora a crescere, e quindi nel grafico, la pendenza della curva dei costi crescerà.
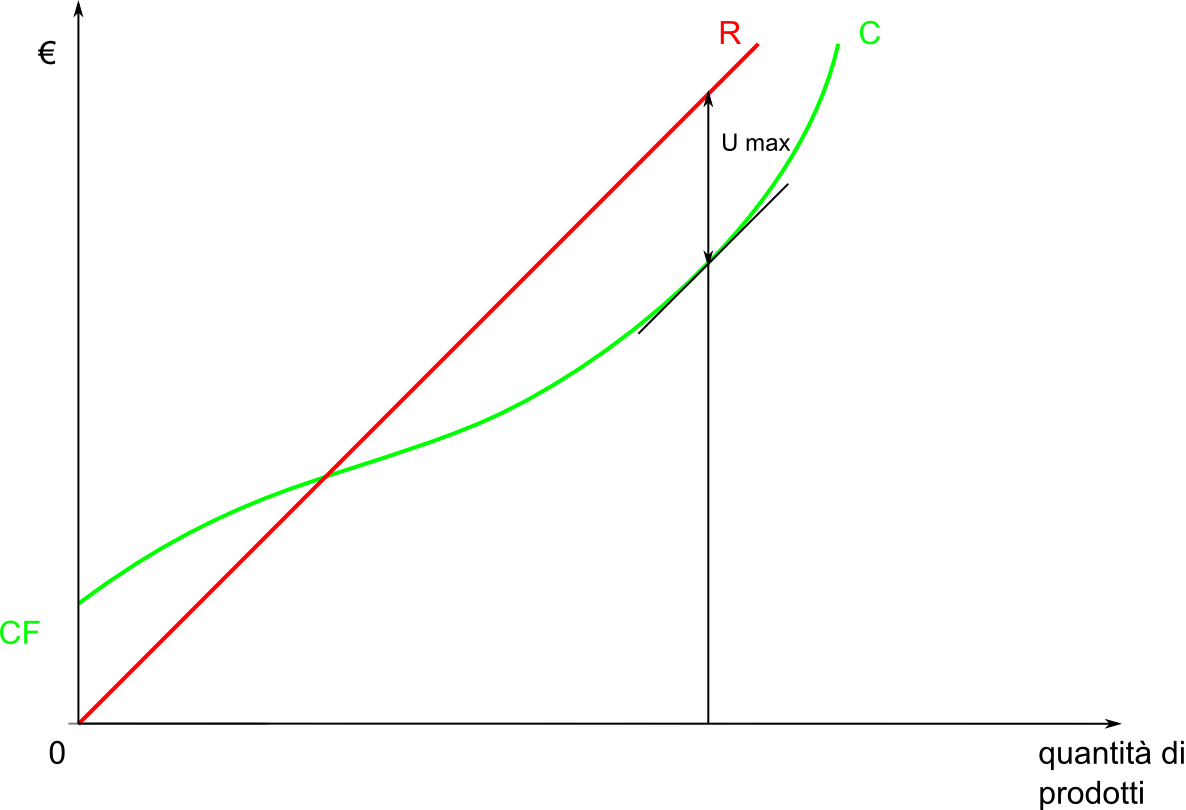
Dal grafico si capisce che ciò avviene quanto il costo marginale eguaglia
il prezzo (essendo i costi marginali rappresentati dalla pendenza della
curva dei costi e il prezzo, se costante, rappresentato dalla pendenza
della retta dei ricavi).
Abbiamo infine fatto l'ipotesi che tutti i prodotti realizzati venissero venduti, ma non è sempre così, ovviamente, ci sarà dell'invenduto, e questo ovviamente costituisce un mancato ricavo, quindi a sua volta un costo. Ciò che non viene venduto fa parte delle rimanenze di magazzino, di cui fanno parte anche ad esempio le materie prime acquistate e non utilizzate, e al termine del periodo considerato, costituiscono un costo.
Pertanto in questo caso Qr è diverso da Qv, e l'utile sarà dato da:
U = P*Qv - CM*Qr - CF
e se chiamiamo Qi la quantità invenduta,
ossia:
Qi = Qr - Qv
per cui:
Qv = Qr - Qi
risulterà:
U = P*Qr - P*Qi - CM*Qr - CF
ossia:
U = (P - CM) * Qr - CF - P*Qi
dove si vede che la quantità invenduta porta, ovviamente, a una diminuzione degli utili
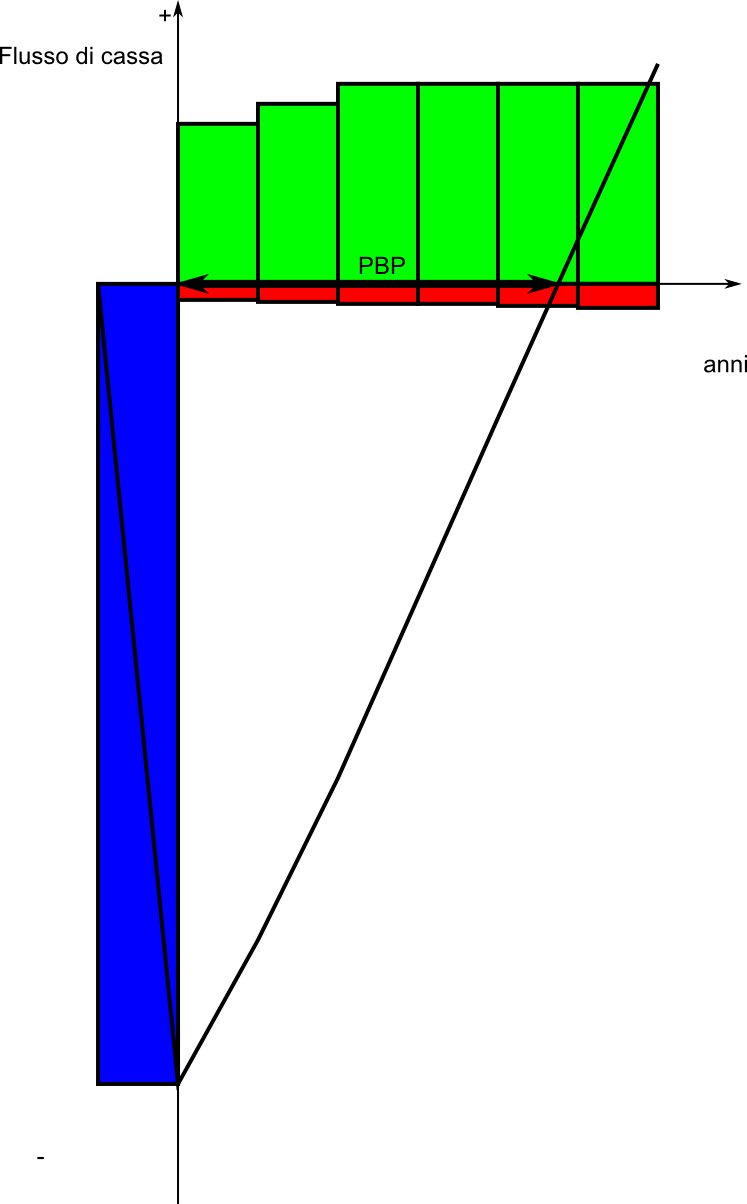
Il periodo di rimborso ("Pay Back Period", anche indicato con l'acronimo PBP in inglese), o anche periodo di ritorno dell'investimento, indica il tempo, espresso in anni, in cui l'investimento di un bene strumentale viene recuperato.
In altre parole è il tempo in cui i flussi di cassa cumulati eguagliano l’investimento iniziale. Per flusso di cassa cumulato si intende la somma algebrica dei flussi di cassa di più anni.
Il flusso di cassa è l'utile conseguito in un periodo considerato (R-C), tipicamente in un anno. I costi però sono al netto (cioè senza considerare) le quote annue di ammortamento, in quanto l'esborso per l'acquisto dei beni strumentali è considerato prima dell'istante in cui iniziano a produrre utili. Il termine flusso di cassa rende bene evibente il fatto che tali importi siano in entrata (i ricavi) o in uscita (i costi e gli investimenti).
Si consideri, per esempio l'acquisto
di un bene strumentale che comporti un esborso di 20.000€, e il cui
utilizzo comporti annualmente sia dei costi (senza considerare le quote
annue di ammortamento, sia dei ricavi. che vengono rappresentati nella
tabella che segue:
| Anno |
Investimenti |
Ricavi |
Costi |
Utili |
Utili
Cumulati |
| 0 |
20.000 |
0 |
0 |
-
20.000 |
-
20.000 |
| 1 |
0 |
4.000 |
400 |
+
3.600 |
-
16.400 |
| 2 |
0 |
4.500 |
450 |
+
4.050 |
-
12.350 |
| 3 |
0 |
5.000 |
500 |
+
4.500 |
-
7.850 |
| 4 |
0 |
5.000 |
500 |
+
4.500 |
-
3.350 |
| 5 |
0 |
5.000 |
550 |
+
4.450 |
+
1.100 |
| 6 |
0 |
5.000 |
600 |
+
4.400 |
+
5.500 |
In pratica, ogni anno, l'utile cumulato è dato dalla somma degli utili con gli utili degli anni precedenti.
Si vede come gli utili cumulati, nell'esempio considerato, cambino di segno durante il 5° anno di esercizio: in tale esercizio avverrà il recupero dell'investimento.
E' possibile rappresentare questo fatto con un intuitivo diagramma temporale che mostra il flusso di cassa di anno in anno:

Il periodo di rimborso è un parametro utile per giudicare la bontà di un investimento rispetto ad un altro, ad esempio quando si devono confrontare due possibili investimenti. E' sicuramente desiderabile che un investimento abbia un periodo di rimborso breve, ma è anche vero che è un parametro che nulla dice sulla bontà di un investimento dopo che esso è completamente rientrato.
:: Torna all'indice di Organizzazione e gestione dei
processi produttivi ::
